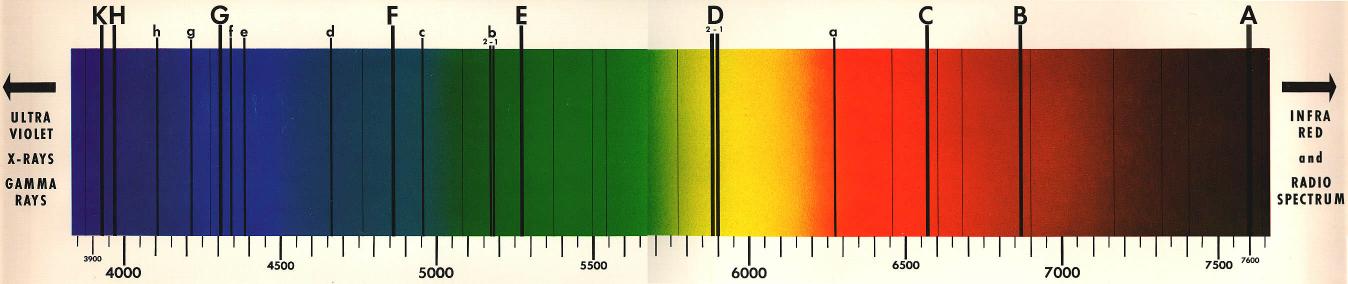
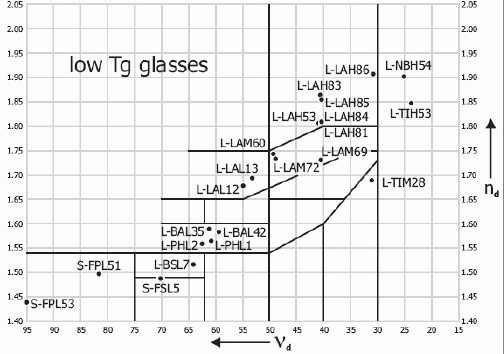
광학기구의 수차

색수차

색깔에 따라 다른 지점에 상을 맺는다.

렌즈를 만드는 매질은 분산 때문에 파장에 따라 굴절률이 달라진다. 따라서 렌즈의 초점거리도 파장에 따라 달라질 수 밖에 없다. 이 수차는 비록 근축광선이라도 나타나기 때문에 색채가 중요한 광학기구, 예를 들어 사진술에서 아주 중요한 수차라고 할 수 있다. 아래 프로그램에서는 유리 등 실제의 매질로 볼록렌즈를 만들었을 때 파장에 따라 상이 맺히는 점이 벗어나는 것을 보여주고 있다. 여기서 구면수차도 (오히려 색수차보다 더 크게) 같이 나타나는 것이 보인다. (프로그램에서 도입한 물질들의 분산특성은 '분산 프리즘'에서 참조할 수 있다)

위 프로그램에서 살펴볼 수 있는 것처럼 렌즈 매질이 분산을 가지고 있는 한 하나의 렌즈로 색수차를 없애는 것은 불가능하다. 렌즈를 만드는 모든 물질이 파장이 줄어들면 굴절률이 줄어드는 정상분산이므로 붉은 빛에서 푸른 빛으로 가면 초점이 렌즈 쪽으로 다가가게 된다. 만일 위 그림에서 잘록한 허리에 스크린을 놓는다면 붉은 색은 미쳐 빛이 모여들기 전이므로 넓은 원판이 되고, 보라색에 대해서는 초점을 지나쳐서 역시 넓은 원판을 만들 것이다. 이 지점으로부터 점차 스크린을 멀리 보내면 이제 노랑, 녹색, 보라의 순으로 원판이 더 넓게 퍼진다.

_ 분산 프리즘_ 정상분산_ 근축광선_ 광선추적_ 볼록렌즈_ 초점거리_ 굴절률_ 전이

색지움

렌즈를 조합해서 색수차를 줄인다.

분산특성이 다른 렌즈를 조합해서 색수차를 상당한 수준으로 줄일 수 있다. 당연히 볼록렌즈끼리는 불가능하고, 볼록과 오목을 결합해서 가능하다. 이렇게 둘 이상의 렌즈로 색수차를 줄이는 과정을 색지움(achromatism)이라 한다. 다음 그림은 이렇게 맞춘 렌즈의 조합을 보여주고 있다.

아무리 렌즈를 조합하더라도 모든 파장에 대해 색지움하는 것은 불가능하다. 따라서 대표적인 두 파장을 선택하게 되는 데 보통 분광선 중에서 프라운호퍼 선에서 고른다. 이 중에서 붉은 색의 $C$-선(656.2816 nm)과 푸른 색의 $F$선(486.1327 nm)에 대해 색지움을 하고, 이들의 중간에 있는 노랑의 $d$-선($D_3$-선, 587.5618 nm)을 대표 파장으로 해서 초점거리를 표시하거나 분산의 정도를 나타내게 한다. 예를 들어 분산의 정도를 나타내는 다음 양을 아베수(Abbe number)라 하고 이 값이 크면 분산이 상대적으로 작은 값이어서 단일 렌즈로는 색수차가 작게 나타날 것이다. $$V_d = \frac{n_d - 1}{n_F - n_C}$$ 여기서 각 파장에 대한 굴절률을 첨자로 표시하였다. 보통 아베수는 $d$-선을 기준으로 하기 때문에 $V_d$로 표시하는 데 이와 달리 $D$-선(Na의 589.3 nm)이나 $e$-선(Hg의 546.07 nm)을 기준으로 하면 각각의 아베수를 $V_D$, $V_e$로 표기한다.

photo

프라운호퍼선_ 태양의 스펙트럼으로 흡수스펙트럼 선을 $C, D_3, F$ 등으로 나타내고 있다.

다음 그림은 렌즈의 제작에 널리 쓰이는 여러 종류의 광학유리에 대해 아베수와 $n_d$를 도표로 나타낸 것이다. 그림에서 사용한 기호는 Ohara 사의 것으로 본 교재에서 사용하는 Schott 사의 표기와의 대응관계도 큰 그림에서는 보여준다.

graph

굴절률과 아베수 도표_ 각종 유리에 대해 가로축을 아베수 $v_d$, 세로축을 굴절률 $n_d$로 그린 도표이다. 큰 그림으로 각 계열에 대해 보다 자세한 도표를 볼 수 있다.

이제 두 물질로 이루어진 볼록-오몰렌즈의 복합렌즈를 생각해 보자. 각각의 매질의 파장별 굴절률은 $n_{1C}$, $n_{2d}$ 등으로 표시하고, 각 파장에 대한 초점거리를 $f_{1F}$ 등으로 표시하기로 한다. 두 렌즈는 얇은 렌즈로서 서로 밀착시켰다고 하면 복합렌즈의 초점거리의 관계식 $$\begin{equation} \label{eq2} \frac{1}{f} = \frac{1}{f_1} + \frac{1}{f_2} \end{equation}$$ 을 각각의 파장에 대해 쓸 수 있다. 합성초점거리를 $C$-선과 $F$-선에 대해 일치시키려면 $$f_{C} = f_{F}$$ 즉, $$\begin{equation} \label{eq4} \frac{1}{f_{1C}} + \frac{1}{f_{2C}} = \frac{1}{f_{1F}} + \frac{1}{f_{2F}} \end{equation}$$ 을 만족해야 한다. 한편 다음의 렌즈의 제작자 공식을 환기하자. $$\frac{1}{f} = \left(\frac{R_2 - R_1}{R_1 R_2}\right) (n-1) = \rho (n-1)$$ 마지막 항의 $\rho$는 한 렌즈가 가진 두 곡률반경 $R_1$과 $R_2$로 계산되는 값이다. 이를 $\eqref{eq4}$ 식에서의 각각의 $f$에 적용하면 다음으로 정리된다. $$\begin{equation} \label{eq6} \frac{\rho_1}{\rho_2} = - \frac{n_{2F}-n_{2C}}{n_{1F}-n_{1C}} \end{equation}$$ 이 식을 만족하는 두 렌즈를 조합하면 $C$와 $F$ 두 색에 대해서는 '색지움'이 된다. 이것으로도 도움이 될 수 있겠지만 이를 아베수로 정리해 두는 것이 여러모로 편리하다. 이를 위해서 표준 파장이라 할 수 있는 $d$-선에 대해 $\rho$의 비를 나타내자. $$\begin{equation} \label{eq7} \frac{\rho_1}{\rho_2} = \frac{(n_{2d}-1)}{(n_{1d}-1)} \frac{f_{2d}}{f_{1d}} \end{equation}$$ $\eqref{eq6}$과 $\eqref{eq7}$에서 $\rho$의 비를 소거하면 다음과 같이 아베수의 관계로 정리된다. $$V_{1d} f_{1d} + V_{2d} f_{2d} = 0$$

실제 렌즈를 설계하면서 아베수가 서로 다른 두 물질을 고르면 우선 이 관계가 만족되어야 한다. 아울러 복합렌즈의 합성초점거리 관계인 $\eqref{eq2}$ 식도 만족해야 하므로 이제 각각의 초점거리 $f_{1d}$와 $f_{2d}$를 결정할 수 있게 된다. 이와 같이 설계하면 $C$와 $F$-선에 대해서는 공통의 초점을 갖지만 $d$-선에 대해서는 아니다. 비록 $d$-선이 $C$와 $F$ 사이에 있으므로 이들의 초점이 크게 벗어나진 않겠지만 엄밀하게 $f_d$는 단지 설계를 위해서 도입하는 기준 초점거리이다.

[질문1] 앞의 식들로부터 $f_d$의 합성초점거리를 갖는 색지움 렌즈의 각각의 초점거리 $f_{1d}$, $f_{2d}$를 $f_d$와 아베수 $V_{1d}$, $V_{2d}$로 나타내어라.

[질문2] 색지움의 두 렌즈의 곡률반경을 너무 작게 하지 않기 위해서는 아베수의 격차가 큰 물질을 골라야 한다. 이 이유를 설명하라.

[질문3] 아베수가 각각 50 과 25 인 두 물질로 초점거리 100 cm 인 렌즈를 만든다고 하자. 두 렌즈의 초점거리는 각각 얼마이어야 하는가? 만일 이들의 굴절률 $n_d$가 1.6, 1.8 이고, 두 렌즈를 평면으로 접촉하게 한다면 다른 한쪽의 곡률은 각각 얼마로 제작해야 하는가?

[질문4] 두 렌즈로 두 파장에 대해 색지움할 수 있다. 세 렌즈의 조합으로 세 파장에 대해 색지움할 수 있을까?

_ 렌즈의 제작자 공식_ 프라운호퍼 선_ 흡수스펙트럼_ 렌즈의 조합_ 광선의 행동_ 얇은 렌즈_ 볼록렌즈_ 오목렌즈_ 초점거리_ 굴절률_ 분산