방사성붕괴법칙

방사성붕괴법칙

방사성 원자핵은 붕괴에 대한 기억을 가지고 있지 않다.

분열 가능한 핵, 즉 방사성 동위원소(radioactive isotope)가 언제 분열하는가는 핵의 종류에 따른 특정한 확률에 의해 결정된다. 알파붕괴의 경우에 대하여 생각해 보자. 핵 속에 있는 알파 입자 덩어리는 핵의 가장자리에 형성되어 있는 에너지 장벽 때문에 그 내부를 끊임없이 왕복운동을 하게 된다. 그러나 양자역학에 의하면 높은 에너지 장벽을 박차고 탈출할 수 있는 적은 확률이 있기 때문에 알파붕괴를 할 가능성을 가지고 있다. 이는 전적으로 양자역학적 원리에 지배되기 때문에 이 확률은 일정한 값으로 정해진다. 알파 입자가 상당히 오랫동안 붕괴하지 않고 왕복운동을 하였더라도 그 다음에 붕괴할 확률은 처음으로 부딪혔을 때와 마찬가지이다. 주사위를 '6'이 나올 때까지 던지는 실험을 생각해 보자. 상당히 오랫동안 '6'이 나오지 않았다고 1회 시도에서 '6'이 나올 확률이 점점 커지는 것은 아니다. 알파붕괴도 이처럼 지금까지 붕괴를 시도한 데 대한 기억을 가지고 있지 않기 때문에 이것이 나름대로의 붕괴의 양상을 결정한다.

이렇게 양자역학의 지배를 받는 것은 알파붕괴뿐만 아니라 모든 붕괴가 다 마찬가지다. 즉, 하나의 핵에 대한 변화가 특별한 외부의 자극이나 인접한 핵의 영향이 없이 순전히 자발적으로 일어나는 경우에는 그 반응은 일정한 확률로 일어나게 되는 것이다.

_ 동위원소_ 양자역학_ 알파붕괴

핵의 붕괴곡선

확률에 의한 반응의 결과로 지수함수 꼴로 생존한다.

하나의 핵이 1초당 붕괴할 확률을 $\lambda$ 라고 하자. 이것을 붕괴상수(decay constant)라 하며, 이 값은 핵이 놓여 있는 외부 조건에 거의 무관하다. 핵은 전자의 구름에 의해 감싸여 있어, 일상적인 온도, 압력, 화학반응 등 조건에서 핵은 무풍지대로 남아 있어 핵의 상태는 영향을 전혀 받지 않기 때문이다.

$N$ 개의 핵이 있었다면 이 $N$ 개의 핵 중에서 $dt$ 초 동안에 붕괴하는 개수(즉, $-dN$)는 $\lambda N dt$ 일 것이다. 따라서 다음의 미분방정식을 만족한다. \[ \begin{equation} \label{eq1} \frac{dN(t)}{dt} = -\lambda N(t) \end{equation} \] $N(t)$에 대하여 이 방정식을 풀어보면 \[ N(t) = N_0 e^{-\lambda t} \] 이 함수는 지수함수적으로 감소하는 함수로서 $N_0$는 $t=0$ 시간에 주어진 핵의 개수이다. 지수함수는 시간에 따라 나머지의 일정한 비율로 줄어드는 특성을 가진다. 따라서 처음의 반으로 줄어드는 시간을 반감기(half life)라 하며 이 값은 잔존하는 핵의 수에 관계없이 일정하다.

반감기는 앞 식에서 지수함수 부분이 1/2 로 되는 데 소요되는 시간이 되어 다음과 같이 붕괴상수에 반비례한다. \[ T_{\frac{1}{2}} = \frac{\ln 2}{\lambda} \approx \frac{0.693}{\lambda} \]

graph

방사성 붕괴 그래프_ 방사성동위원소가 반감기 단위의 시간이 지남에 따라 그 반만 남아있는 것을 그린 그래프이다. 2 반감기에는 1/4, 3 반감기에는 1/8 등으로 한 반감기를 지날때마다 1/2씩으로 줄어든다. 마젠타(심홍색)로 표시한 막대는 어미핵, 녹색의 막대는 붕괴 결과로 생성된 딸핵의 분량을 나타낸다.

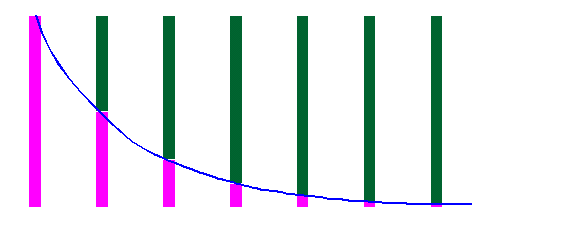
위 그래프에서 처음에 있던 방사성 동위원소가 붕괴하면서 시간에 따라 그 양이 감소하는 추이를 보여주고 있다. 1 반감기에 반이 붕괴하여 딸핵(daughter nuclide)으로 변한다. 따라서 원래의 동위원소와 딸원자핵의 함량의 비율을 측정하면 경과시간을 알 수 있을 것이다.

평균수명은 한 핵의 수명에 대한 기댓값으로 붕괴상수의 역수이다.

반감기는 핵의 개별적인 특성이기는 하지만 많은 수의 핵에 대해서 정의되는 개념이다. 이와 달리 한 핵에 대한 특성으로 그것이 붕괴를 하기까지 걸리는 평균 시간으로 평균수명(mean lifetime)을 정의한다. $N_0$개의 핵이 있을 때, 각각은 $0$으로부터 $\infty$ 시간까지 살아 있을 수 있다. 그중 $t\sim t+dt$ 시간에 붕괴하는 핵은 $t$의 수명을 가지는 것으로 볼 수 있다. 이러한 핵의 수는 \eqref{eq1} 식에 의해 $\lambda N dt$이고, 평균수명은 수명 $t$에 대한 기댓값으로 다음과 같이 계산된다. \[ \tau = \langle t \rangle = \frac{1}{N_0}\int^{\infty}_0 t \cdot \lambda N dt = \lambda \int^{\infty}_0 t e^{-\lambda t} dt = \frac{1}{\lambda} \] 즉, 평균수명은 붕괴상수의 역수로서 반감기와의 관계는 다음과 같다. \[ \tau = \frac{T_{1/2}}{\ln 2} \approx 1.44 T_{1/2} \]

[질문1] 라듐의 반감기가 1600 년일 때 4800 년 후 라듐의 몇 %가 붕괴할까?

[질문2] 반감기의 5 배와 평균수명의 4 배 중 어떤 것이 더 길까?

[질문3] 평균수명 만큼의 시간이 지났을 때 전체 핵의 몇 %가 생존하고 있을까?

[질문4] $^{238}_{~~92}\mathrm{U}$의 원자핵 속의 알파입자는 매초 5 x 10²⁰번 충돌한다. 그리고 핵 내부의 파동함수에 대한 바깥의 파동함수의 비율이 10^-19이라고 하자. 이 핵이 1초 동안 붕괴할 확률은 얼마일까? 또한 이 핵의 평균수명을 구하라.

[질문5] 지구의 우라늄 광산에는 $^{238}_{~~92}\mathrm{U}$과 $^{235}_{~~92}\mathrm{U}$가 0.993:0.007 의 비율로 존재한다. 그리고 각각의 수명은 6.52 x 10⁹년, 1.02 x 10⁹년이다. 대폭발 이후 지구가 형성될 때 이들 우라늄이 1:1의 비율로 존재했다면 지구의 나이는 얼마일까?

_ 동위원소_ 파동함수_ 어미핵_ 기댓값_ 온도_ 딸핵

동위원소의 생성과 붕괴

계속해서 방사성 동위원소가 생겨나면서 붕괴한다.

방사성 동위원소 $^{24}_{11}\mathrm{Na}$는 $^{23}_{11}\mathrm{Na}$에 중성자를 쏘여서 만들 수 있다. 이처럼 어떤 핵에 중성자나 다른 입자를 조사하여 방사성 동위원소를 계속 생성시킨다면 동위원소는 시간에 따라 어떻게 변할까? 생성하는 과정에서도 역시 동위원소는 계속 붕괴하기 때문에 어떤 시점에 이르러 평형을 이룰 것으로 생각할 수 있다. 예를 들어 붕괴상수 $\lambda$인 어떤 동위원소가 단위시간당 $P$의 비율로 생성된다면 $N(t)$는 다음을 만족한다. \[ \frac{dN}{dt} = P - \lambda N \] 이 식은 \[ \frac{dN}{P-\lambda N} = dt \] 로 재배치하여 양쪽을 적분하면, \[ N(t) = N_0 e^{-\lambda t} + \frac{P}{\lambda} (1- e^{-\lambda t}) \] 이다. 이는 반감기의 몇 배에 해당하도록 시간이 충분히 흐르면 거의 평형을 이루는 것을 말한다. 즉 긴 시간이 흘러 $N=\frac{P}{\lambda}$이 되면 새로 생겨나는 동위원소와 줄어드는 동위원소가 같아져서 일정한 수를 유지하고, 이때의 단위시간당 붕괴하는 수는 $P=\lambda N$으로 생성비율과 붕괴비율이 같아진다.

[질문1] $^{23}_{11}\mathrm{Na}$에 중성자를 쏘여서 $^{24}_{11}\mathrm{Na}$를 초당 백만 개 생성시킨다고 하자. 이 경우 최종적으로 단위시간당 붕괴하는 수는 얼마인가? 단 $^{24}_{11}\mathrm{Na}$는 베타붕괴를 하며 반감기는 14.96 년이다.

_ 동위원소_ 베타붕괴_ 중성자