푸리에 해석

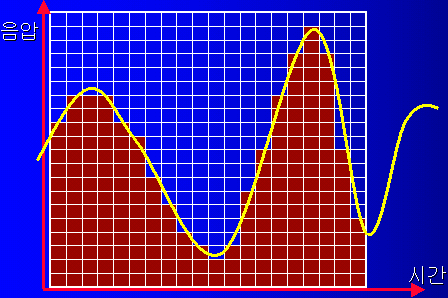
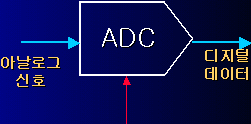
디지털 푸리에 변환

파동의 성분을 알아낸다.

한 지점에서의 파동의 움직임을 계속 관측하면 주어진 각각의 시간에 파동량의 그래프를 그릴 수 있을 것이다. 이 그래프는 모든 시간 값에 대하여 대응되는 파동량을 가지고 있는 아날로그의 데이터일 것인 데 이 신호를 컴퓨터를 통해서 읽으면 띄엄띄엄한 시간에 띄엄띄엄한 파동량의 디지털화 된 데이터로 될 것이다.

예를 들어 소리의 전기신호를 오실로스코프로 보면 음압이나 변위에 대한 연속적인 그래프가 화면에 바로 나타날 것이다. 이 신호를 푸리에 해석을 하여 주파수 성분을 추출하고자 한다면 앞에서 설명한 대로 여러번 적분을 행해야 할 것이다. 그러나 음압을 나타내는 전기신호는 보통 해석적인 함수가 아니므로 해석적으로 적분을 할 수 없게 되어 수치해석이 필요해진다. 콘덴서나 코일 등의 소자를 구성해서 아날로그로의 푸리에 해석을 어느 정도는 해 낼 수 있지만 엄밀한 분석은 불가능하다.

컴퓨터를 이용한 신호분석

음파의 신호를 컴퓨터를 통해서 읽게 되면 수치해석을 컴퓨터의 연산능력으로 푸리에 해석을 할 수 있게 된다. 이 경우 컴퓨터는 신호의 변화에 대하여는 매우 짧은 시간간격이긴 하지만 어떤 유한한 간격으로 신호를 읽을 수밖에 없을 것이다. 측정의 시간 간격을 줄이면 줄일수록 원래의 아날로그 데이터에 근접하게 되겠지만 같은 시간분량에 대한 데이터 수는 시간간격에 반비례하여 늘어가게 되어 컴퓨터가 감당하지 못하게 된다. 한편 어떤 시간의 측정 값도 당연히 디지털화 된 신호일 수밖에 없다. 따라서 연속적인 모든 값을 표현하지 못하고 불연속적인 값들 중 하나로 나타내어지게 된다. 시간 축으로나 신호 축으로나 이렇게 띄엄띄엄하게 측정되는 것을 양자화되었다고 한다.

graph

음파의 샘플링_ 시간에 따라 변하는 음압값은 그림에서 노란 곡선처럼 연속적으로 변하는 아날로그 값이다. 음성분석이나 음향분석을 위해서는 주기적이 아닌 이 신호를 분석하기 위하여 데이터를 컴퓨터에서 읽어야 한다. 이렇게 아날로그 신호를 디지털 데이터로 읽는 장치를 아날로그-디지털 변환기(ADC)라고 한다, 신호의 세기 측면에서나 시간 측면에서 다 같이 샘플링 과정에서 위 그림처럼 띄엄띄엄하게 값을 읽을 수 밖에 없다. 이를 양자화라 한다.

음악을 기록한 것 중 옛날의 LP 판은 음파의 변화를 연속적으로 기록해 둔, 일종의 아날로그형의 신호 기록으로 볼 수 있고, CD나 DAT 등은 음파를 디지털화시켜 기록한 것으로 비교해 볼 수 있다. CD의 경우 1초에 4만번 이상으로 한 번에 16비트, 즉 6만 계단 이상으로 음을 기록해서 이를 재생하면 아날로그의 원형을 거의 완벽하게 재생해 낼 수 있게 된다. 아날로그 기록인 경우 신호가 정확하게 읽혀지지 않을 가능성이 있지만 값으로 기록된 디지털 기록은 언제나 정확하게 읽혀지게 되고 통신을 통해서도 정확하게 전달 시킬 수 있게 된다.

디지털화된 신호는 { 1.1, 1.2, 1.34, ... } 처럼 일종의 수열로서 시간 순서로 이루어져 있다면 시계열(time series)라고 한다. 이 데이터를 이제 컴퓨터에서 수치해석으로 적분하여 그 신호가 가지고 있는 각각의 주파수 성분, 즉 스펙트럼을 계산해 낼 수 있게 된다. 이에 관련된 기법을 DFT(discrete fourier transformation)라 하여 디지털 신호처리(DSP: digital signal processing) 기술의 핵심을 이루게 된다. 즉 음성인식이나 변조, 복원 등 여러 가지 기법이 DSP를 통해서 가능하게 되었다.

_ 수치해석_ 파동량_ 양자화_ 음파_ 주기

FFT 해석

매우 빠르게 푸리에 분석을 수행한다.

분석해야 할 시계열의 데이터가 $N$이라 한다면 이를 DFT를 통해서 푸리에 변환하기 위해서는 $N^2$의 복소수 곱셈을 해야 된다. 예를 들어 1초당 1000 번 측정한 신호의 1 초간의 데이터를 한꺼번에 변환하기 위해서는 $10^6$ 번의 복소수 곱셈을 해야 하므로 컴퓨터가 이를 계산해 내는 데 상당한 시간이 필요로 하게 된다.

한편 데이터가 $N = 2^m$, 즉 2, 4, 8, 16, ... , 1024, ... 로 되어 있다면 계산량을 획기적으로 줄일 수 있는 방법이 개발되었다. 이를 빠른 푸리에 변환, 즉 FFT(fast fourier transformation)라고 한다. FFT를 통해서는 $Nm/2$ 번의 복소수 곱셈이 필요하여 예를 들어 1024 개의 데이터를 변환하는 데 5000 번이 된다. 이는 DFT에 비해서 1/200 정도로 계산량이 줄어든 것인 데 데이터 개수가 많아질수록 그 줄어드는 비율은 커진다.

아래 프로그램은 주어진 몇 가지 파형에 대하여 FFT로 푸리에 변환하여 그 결과, 즉 스펙트럼을 그래프로 나타내게 된다. 위쪽 그림은 시간에 대한 신호의 그래프이고, 중앙의 그림은 이의 스펙트럼 그래프이다. 신호는 1초에 8000 번 측정된 것으로 생각하자. 이 경우 가운데의 스펙트럼 그래프의 주파수 축인 가로축의 최대 값은 4000Hz가 된다. 샘플링 데이터 수로 선택하게 되어 있는 값이 바로 FFT에 계산되는 데이터 수로서 이 값은 언제나 $2^m$형으로 되어 있는 것을 알 수 있을 것이다. 이 값을 변화시켜서 분석결과가 어떻게 달라지는 지를 관측해 보자. 또 파형의 형태나 그 주파수 값, 포함되어 있는 직류성분, 노이즈의 정도 등을 변화시키면서 그 변환결과가 변하는 것을 관측해 보자.

여기서 변환 결과가 주된 피크 주위에 잇따라 줄어드는 피크가 있는 것을 보일 때가 있다. 이는 FFT의 특성상 $N$개의 데이터가 계속해서 반복되어 있는 주기함수의 푸리에 변환 결과이기 때문이다. 예를 들어 정현파로서 480Hz로 조절하면 실제로 480Hz의 피크 주위에 작은 피크들이 생겨난다. 이 경우 480Hz의 정현파가 반복되어 있는 주기함수로서 끝이 불연속으로 이어진 정현파의 누더기와 같은 파의 푸리에 변환이기 때문이다. 이 경우 데이터 개수를 늘여주면 그 스펙트럼의 폭이 줄어드는 것을 알 수 있을 것이다. 한편 위 신호 그래프에는 $N$개의 데이터 전체를 나타낸 것으로서 예를 들어 $N=256$ 이라면 256/8000초의 데이터가 전체 그래프로 표시되어 있다.

_ 진동수_ 복소수_ 주기_ 보일