레이저의 원리

결맞은 빛을 방출하기 위해서는 대부분의 빛을 자극에 의한 방출로 채워야 하고 이러기 위해서는 높은 에너지 준위(energy level)에 있는 원자의 수를 많게 해야 한다. 이를 밀도반전(population inversion)이라고 한다.

물질이 이러한 밀도반전의 상태가 되면 수많은 높은 에너지 상태의 원자 중 한 개가 어쩌다가 자발적으로 빛을 내는 순간 여기서 방출된 빛이 주변의 다른 들뜬 원자 하나를 자극하여 빛을 내게 하여 결국 두 개의 광자가 된다. 또 이 두 개는 다른 두 원자를 자극하여 네 개가 되고, ... 이러한 연쇄적인 과정에 의해 기하급수적으로 결맞는 빛의 개수가 성장하게 된다. 이를 레이저 발진이라 한다. 이러한 일이 일어날 수 있도록 물질의 상태를 만드는 일은 바로 레이저를 가능하게 하는 관건이 된다.

그러나 통상적인 열적평형상태에 이렇게 밀도를 반전시키는 것은 불가능하다. 이용할 정도의 밝기의 빛을 내기위해서는 이에 관여하는 원자의 수가 아보가드로 수 정도로 매우 많아야 하고, 따라서 에너지 준위

$E_1$ ,

$E_2$ ,

$E_3$ 등의 상태에 있을 확률은 그 에너지 값과 온도에의해 결정된다. 온도

$T$ 로 열적 평형상태에 있는 원자에서

$E$ 의 에너지 준위에 있을 확률은

$P(E)=Ce^{-E/kT}$ 여기서

$k$ 는 볼츠만 상수로

$k=1.38\times 10^{-23}\mathrm{J/K}=8.62\times 10^{-5}\mathrm{eV/K}$ 이고

$C$ 는 전 에너지 준위에 대한 확률을 합하면 1이 되게 하는 상수이다. 이렇게 에너지 값이 커지면 그 확률이 지수함수적으로 줄어들어야 한다는 것은 볼츠만(L. E. Boltzmann)이 열역학을 통계역학적인 관점에서 연구하여 알아낸 것이다. 이에 의하면

$E_1$ 과

$E_2$ 의 두 에너지 준위에 있는 원자 수의 비는

$\frac{n_2}{n_1}= e^{-(E_2-E_1)/kT}$ 이므로 온도가 올라가면 높은 에너지 준위에 있는 원자 수가 상대적으로 많아지지만 온도가 무한대가 되더라도 원하는 반전의 상황은 일어나지는 않는다. 위 볼츠만의 관계식으로 반전이 되는 온도를 억지로 추정한다면 음의 온도상태이나 음의 온도는 있을 수 없다. 따라서 통상적인 원자의 에너지 준위사이에서는 반전이 결코 일어날 수 없고 특별히 어떤 원자에서 에너지 준위사이를 특이하게 전이가 선택적으로 일어나는 경우에는 가능해질 수 있다.

2 준위만으로는 반전 불가

근본적으로 반전시키는 것은 불가능하다. 아래 그림에서 오직 두 개의 준위만 개입시켜 반전을 만드는 것을 생각해보자. 낮은 에너지 준위에서 높은 에너지 준위로 올려주기 위하여 외부에서 에너지를 공급하는 것을 광펌핑(optical pumping)이라 한다.

펌핑을 맹렬히 하게 되면 높은 상태로 빨리 올라가기는 하나 이 들뜨게 된 원자가 많아질수록 그 원자수에 비례하여 더 큰 확률로 자발적 방출에 의해 낮은 에너지 상태로 내려 와버리게 된다. 원자의 전이에서 펌핑으로 올려보내는 것이 가능하면 역시 떨어지는 것도 가능하게 되어있고 실제로 이들 두 가능성, 즉 전이확률은 비례한다. 마치 밑이 빠진 독에 물을 퍼 담는 것과 같이 많이 퍼 담으면 또한 많은 물이 빠져 버려 결국 아무런 물도 고이지 않는 경우와 유사하다.

graphic

2 준위 원자_ 원자의 에너지 준위 두 개 사이에서 다른 준위와 독립적으로 전이를 하는 상황에서 언제나 낮은 에너지 준위에 더 많은 원자가 있게 된다. 이는 열적 평형조건 때문으로 이러한 경우는 유도방출의 비율이 낮아 레이저 발진이 일어나지 않는다.

ani

2 준위 원자_ 여러 원자가 놓여있는 에너지 상태를 그림으로 표현한 것으로 원자들이 상태를 넘나들고 있다. 여기서는 원자의 여러 에너지 준위중 오직 두 준위만 관여하는 경우에 대한 것으로 여기된 원자는 바닥상태로 떨어져 버린다. 펌핑을 빨리시키면 빠르게 바닥상태로 되돌아와 버리기 때문에 낮은 준위에 더 많은 원자가 몰려 있게 되어 밀도반전이 근본적으로 불가능하다.

3준위 - 반전가능

반전시키는 것이 가능하다. 단 이를 위하여 그 세 준위 사이에는 특이한 관계가 있어야 한다. 아래 그림에서

$E_2$ 에서

$E_1$ 으로 전이하는 것이 거의 금지되어 있다고 하자. (양자역학으로 그 확률을 계산할 수 있고 금지된 경우 그 확률이 거의 0이다. 이렇게 양자역학으로 그 전이가 허용되는 경우의 규칙을 선택규칙(selection rule)이라 한다)

또한 그림에서 제일 높은 세 번째 에너지 준위에서는 빠르게

$E_2$ 준위로 전이한다고 하자. 광펌핑에 의해서 제일 높은 상태의 들뜬원자는 빠르게

$E_2$ 준위로 내려가게 되나, 거기서 바닥상태로의 전이가 금지되어 있기 때문에 많은 원자가 그 상태에 머물게 될 것이다. 이렇게

$E_2$ 와

$E_1$ 의 두 준위를 놓고 보면 밀도가 반전된다.

graphic

3 준위 원자_ 원자의 세 개의 에너지 준위가 관련되어 그중 두 준위 사이에서 반전을 시킬 수 있다. 이러한 조건에 이르게 하기 위해서는 확률이 매우 작아 금지된 전이가 있어야 하는 데 그림에서는 'Laser Transition'으로 표시한 전이가 이에 해당한다.

ani

3 준위 원자의 펌핑과 밀도반전의 과정_ 여러 원자가 놓여있는 에너지 상태를 그림으로 표현한 것으로 원자들이 상태를 넘나들고 있다. 여기서는 금지된 전이가 있어 반전이 가능한 3준위 원자에서 바닥상태의 원자가 펌핑에 의해 맨 위 준위로 올라가서 빠르게 두 번째로 전이하게 된다. 두 번째 준위에 머물고 있는 원자들은 외부의 자극에 의해 일거에 유도방출을 하게 된다. 그림처럼 레이저 전이가 연속적이지 않고 일시에 일어나게 되면 레이저는 짧은 시간 동안 지속되어 펄스 레이저가 된다. 한편 그림과는 달리 이러한 순환과정이 연속적으로 일어나게 되면 레이저가 지속적으로 나오는 연속발진 레이저가 된다.

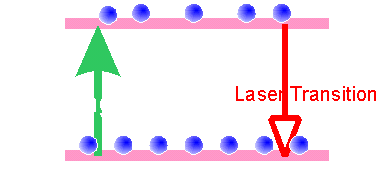
4준위 - 반전가능

반전시키는 것이 가능하다. 단 이때는 아래 그림처럼 네 준위가 적당히 선택되기도 하고 금지되기도 해야 한다.

graphic

4 준위 원자_ 원자의 네 개의 에너지 준위가 관련되어 그중 두 준위 사이에서 반전을 시킬 수 있다. 여기서는 'Laser Transition'으로 표시한 금지된 전이가 하나 있다.

ani

4 준위 원자의 펌핑과 밀도반전의 과정_ 여러 원자가 놓여있는 에너지 상태를 그림으로 표현한 것으로 원자들이 상태를 넘나들고 있다. 여기서는 맨 위 준위로부터 그 아래 준위( $N_2$ 로 표시한)로의 전이와 세 번째의 준위( $N_1$ 로 표시한)로부터 바닥상태로의 전이는 빠르게 일어나고, 가운데 두 준위에서는 전이가 금지되어 있다. 따라서 언제나 $N_2$ 에는 많은 원자가, $N_1$ 에는 적은 수의 원자가 있어 3준위에 비하여 밀도반전의 정도가 심해진다. $N_2$ 의 원자들은 외부의 자극에 의해 일거에 유도방출을 하게 된다. 그림처럼 레이저 전이가 연속적이지 않고 일시에 일어나게 되면 레이저는 짧은 시간 동안 지속되어 펄스 레이저가 된다. 한편 그림과는 달리 이러한 순환과정이 연속적으로 일어나게 되면 레이저가 지속적으로 나오는 연속발진 레이저가 된다.