프레넬 회절

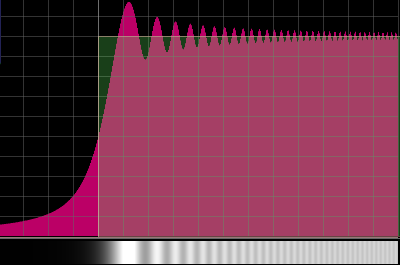
슬릿의 프레넬 회절

슬릿(slit, 실틈)에 대해 코르뉴 나선으로 회절무늬를 계산하는 절차를 알아보자.

이 경우에는 $x$는 전 구간이 열려 있으므로 $u=-\infty \sim \infty$까지 적분을 하면 $1+i$가 되어 다음과 같이 $y$에 대한 적분만이 남는다. \[ \begin{equation} \label{eq1} \Psi_P = \frac{\Psi_0}{1+i}\left[ C(v) + i S(v) \right]_{v_1}^{v_2}. \end{equation} \] 스크린의 각 지점에서의 밝기를 계산하려면 $P$ 점을 옮겨가면서 위 식을 계속 적용해야 한다. 이때 $P$ 점이 이동하면 슬릿이 열려있는 시작점 $v_1$과 끝점 $v_2$가 달라진다. 이는 $P$와 광원을 연결한 직선이 슬릿 면과 만나는 점을 $v$ 좌표의 원점이 삼았기 때문이다. 그러나 그 범위, 즉 $v_2 - v_1$ 값은 일정한 값을 유지하게 된다. 스크린의 위로부터 아래로 내리면서 계산을 한다는 것은 $v_1$를 $-\infty$로 부터 $\infty$ 변화시키면서 \eqref{eq1} 식을 적용하는 것이다.

이 계산은 코르뉴 나선 도형에서는 직관적으로 이해할 수 있다. 즉, $v_1=-\infty$에서 출발하여 $+$ 방향으로 점진적으로 옮기되 슬릿이 열려있는 폭에 대응되는 $v_2 - v_1$값을 일정하게 하여 $v_2$를 같이 옮기면 된다. 이때 두 점을 연결한 벡터의 복소수값이 \eqref{eq1} 식의 오른편 [...]으로 $P$ 점에 도달하는 빛의 위상자가 된다.

이렇게 슬릿에서의 회절을 해석하는 절차를 아래 프로그램에서 보여주고 있다. 주어진 슬릿의 폭에 대해 출발점 $v_1$을 달리했을 때의 결과를 코르뉴 나선 도형 위에서의 위상자의 화살로 나타내고 이의 길이 등 세부 정보를 수치로 보여준다. 아울러 '자동생성'은 스크린의 $P$ 점을 위쪽에서 아래로 내리면서 계속 계산해서 그래프를 완성하게 된다. 여기서 스크린의 아래위는 그래프의 가로축으로 스크린의 위가 그래프의 가로로 $+$ 방향이다.

[질문1] 앞의 그래프는 스크린에 비쳐지는 회절결과를 나타낸 것이지만 가로축은 $v$로서 차원이 없는 양이다. 이를 실제의 길이 축척으로 바꾸는 절차를 설명하라. 또한 이를 이용해서 파장이 변할 때 회절무늬가 변하는 양상을 알아보자.

[질문2] 슬릿에 평면파가 비추어진다. 이때는 슬릿으로부터 스크린까지의 거리가 바로 $L$이 된다. 이 거리를 증가시키면 무늬는 어떻게 변하겠는가? 거리를 같이 두고 빛의 파장을 증가시키면 무늬는 어떻게 변하겠는가?

[질문3] 여기서와 반대로 슬릿 부분이 빛을 차단하고 나머지가 열려있는 것을 생각하자. 이는 머리카락이나 바늘 등 가느다란 막대모양에 빛의 비추어 쉽게 실험해 볼 수 있다. 이를 코르뉴 나선으로 해석하는 절차를 생각해 보자. 이 결과와 이 모양에 대응되는 슬릿의 회절 결과와는 어떠한 관계가 있을까? 이러한 막대와 슬릿을 서로 상보적(complementary)라 하고, 이에 대해 바비네 원리(Babinet's principle)로 설명하고 있다.

[질문4] 코르뉴 나선 도형으로 이중슬릿에 대한 프레넬 회절을 정성적으로 해석하는 절차를 설명하라.

_ 평면파_ 위상자_ 복소수_ 진폭_ 회절_ 슬릿

칼날의 프레넬 회절

칼날이 $y=0$을 따라 아래에 놓여 있으면 열린 구간은 스크린의 각 위치로 정해지는 $v$로 부터 $v=\infty$까지이다. 따라서 언제나 $v_2 = \infty$ 이다. 따라서 \[ \Psi_P = \frac{\Psi_0}{1+i}\left[\frac{1}{2}+\frac{1}{2}i - C(v_1) - S(v_1) \right] \] 이다. 여기서 $v_1$을 $\infty$로 부터 점차 줄여나가면 칼날의 조명되지 않은 부분$(v_1 \gt 0)$부터 경계$(v_1=0)$, 그리고 개방된 위치$(v_1 \lt 0)$의 회절 결과를 볼 수 있다.

앞의 '슬릿과 칼날의 프레넬 회절' 프로그램에서 '칼날 회절' 선택상자를 선택하면 이러한 상황의 회절무늬를 계산하는 절차와 그 결과를 볼 수 있다.

graph

칼날의 회절무늬_ '슬릿과 칼날의 프레넬 회절' 프로그램으로 칼날의 회절무늬를 그려본 결과로서 스크린에 조명되는 모양은 아래의 띠로 나타내었다. 여기서 붉은 색조의 그래프는 진폭으로 칼날의 경계에서는 완전 조명된 것에 비하여 1/2값을 갖는다.

[질문1] $v_1=0$인 상황, 즉 칼날의 경계에서 완전 조명된 경우에 비해서 밝기가 1/4 이 된다. 이는 파면의 한쪽 절반이 가려막히기 때문이다. 이러한 정성적인 분석으로 경계에서의 밝기가 1/4이 되는 것을 검증하라.

[질문2] 칼날에 500 nm의 평면파가 비추어진다. 이로부터 1.0 m 떨어진 지점에 나타나는 회절무늬를 묘사하라.

[질문3] 여기서의 결과를 소리에 대해서 적용해 본다. 즉, 1.0 m의 담이 있고, 이로부터 2.0 m 떨어지고 담과 같은 높이에서 300 Hz 의 단일 진동수의 소리를 낸다. 담 건너 5.0 m 떨어진 지점에서 들리는 소리를 수직방향으로 이동하면서 측정한다. 이동거리에 따른 세기 분포를 앞 '슬릿과 칼날의 프레넬 회절' 프로그램의 '데이터복사'로 복사한 데이터를 이용해서 그래프를 그려보라. 같은 상황에서 소리의 진동수가 3 kHz, 30 kHz일 때 그 결과가 어떻게 달라지는가? 소리의 속도는 340 m/s 이다.

_ 평면파_ 진동수_ 진폭_ 회절_ 슬릿_ 파면