방사성 계열

거듭되는 핵변환

앞에서 방사성 동위원소들이 계속해서 붕괴를 통한 변화를 거치는 방사성 계열을 알아보았다. 각각의 붕괴과정에서 붕괴상수$(\lambda)$가 고유한 값으로 주어지므로 원래의 주어진 핵이나 붕괴과정에서 생성되는 딸핵들의 수는 서로 관련되어 있을 것이다.

예를 들어 붕괴상수가 $\lambda_1$인 핵 A1 이 붕괴를 거쳐 붕괴상수가 $\lambda_2$인 A2 가 되고 최종적으로 안정된 핵 A3가 된다고 할 때 이들 핵의 수 $N_1$, $N_2$, $N_3$는 다음 관계식으로 묘사된다 \[ \frac{dN_1}{dt}= -\lambda_1 N_1, \] \[ \frac{dN_2}{dt}= \lambda_1 N_1 - \lambda_2 N_2, \] \[ \frac{dN_3}{dt}= \lambda_2 N_2 \] 이 세 연립방정식은 방사성붕괴법칙에서 다룬 바 대로 한 원자핵의 붕괴방식에 기초하고 있다. 단지 A1 이 붕괴한 개수만큼 A2 가 생겨나므로 위 두 번째 식처럼 오른쪽의 첫째 항이 A1 이 붕괴한 개수이고, 둘째 항이 A2 가 붕괴하여 A3 로 변한 개수이다. 특히 첫 식은 그 자체로 풀려서 \[ N_1(t)=N_{10} e^{-\lambda_1 t} \] 가 되고 이 결과를 둘째, 셋째에 순차적 적용하면, \[ N_2 = N_{10} \frac{\lambda_1}{\lambda_2 - \lambda_1} ( e^{-\lambda_1 t} - e^{-\lambda_2 t}) + N_{20} e^{-\lambda_2 t}, \] \[ N_3 = N_{10} \left( 1 - \frac{\lambda_2}{\lambda_2 - \lambda_1} e^{-\lambda_1 t} + \frac{\lambda_1}{\lambda_2 - \lambda_1} e^{-\lambda_2 t} \right) + N_{20} (1 -e^{-\lambda_2 t} ) + N_{30}. \] 이다.

만일에 $t=0$에 A1 핵만 $N_{10}$개 있었으며 다른 A2 나 A3는 없었다고 하자. $N_{20}=N_{30}=0$이 되어 시간이 지남에 따라 A2 나 A3의 개수는 다음과 같이 변화된다. \[ \begin{equation} \label{eq1} N_2 = N_{10} \frac{\lambda_1}{\lambda_2 - \lambda_1} ( e^{-\lambda_1 t} - e^{-\lambda_2 t}), \end{equation} \] \[ N_3 = N_{10} \left( 1 - \frac{\lambda_2}{\lambda_2 - \lambda_1} e^{-\lambda_1 t} + \frac{\lambda_1}{\lambda_2 - \lambda_1} e^{-\lambda_2 t} \right). \] 이 경우 A1은 A2가 A3로 붕괴하는 것과 무관하게 정상적인 붕괴방식으로 줄어들지만 A2와 A3는 조건에 따라 늘어나기도 하고, 거의 일정한 값을 유지할 수도 있다.

\eqref{eq1} 식으로 부터 다음과 같이 A2의 방사능 $\mathcal{A}_2 = \lambda_2 N_2$를 A1의 방사능 $\mathcal{A}_1 = \lambda_1 N_1$로 나타내자. \[ \begin{equation} \label{eq2} \mathcal{A}_2 = \mathcal{A}_1 \frac{\lambda_2}{\lambda_2 - \lambda_1} (1-e^{-(\lambda_2-\lambda_1)t}) \end{equation} \] 이를 다시 A1, A2의 반감기 $T_1$과 $T_2$로 나타내면, \[ \begin{equation} \label{eq3} \mathcal{A}_2 = \mathcal{A}_1 \frac{T_1}{T_1 - T_2} \left(1-2^{-\frac{T_1-T_2}{T_1T_2}t} \right) \end{equation} \] 만일 $\lambda_2\gt \lambda_1$일 때 시간이 많이 흐르면 두 핵의 방사능의 비 \[ \frac{\mathcal{A}_2}{\mathcal{A}_1} = \frac{\lambda_2}{\lambda_2 - \lambda_1} = \frac{T_1}{T_1-T_2} \] 가 수렴하는 것을 알 수 있다.

일반적으로 $n$개의 핵이 관련된 방사성 붕괴계열에 대하여서도 앞의 A1, A2, A3 의 3개의 핵이 관련된 경우처럼 연립방정식을 세워 앞에서부터 차근차근 풀이해 볼 수 있다. 이렇게 $n$개의 핵이 계열을 이루며 붕괴할 때의 각각의 핵의 수가 시간에 따라 변하는 일반해를 베이트먼 방정식(Bateman equation)이라 한다.

_ 방사성 동위원소_ 방사성붕괴법칙_ 방사성 붕괴_ 안정된 핵_ 붕괴상수_ 방사능_ 반감기_ 딸핵

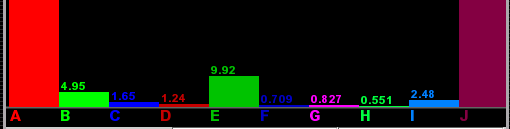
방사성 평형

앞에서 세 핵 A1, A2, A3가 관여하는 두 방정식을 보자. 만일에 \[ \lambda_1 N_1 = 0, ~~ \lambda_1 N_1 = \lambda_2 N_2 \] 이 성립한다면 A1, A2 의 핵의 개수 $N_1$, $N_2$는 변하지 않고 일정한 수를 유지하게 되는 것을 알 수 있다. 이러한 조건에 이르게 된 평형상태를 방사성 평형(radioactive equilibrium)이라 한다. 그러나 위 식에서도 바로 알 수 있듯이 $\lambda_1$ 이나 $N_1$은 0 이 될 수 없으므로 첫째 원소는 줄어들 수 밖에 없다. 만일 $\lambda_1$이 아주 적은 값을 가지고 있다면 $N_1$의 변화를 거의 무시할 수 있게 되고, 아울러 $\lambda_1N_1=\lambda_2N_2$이라면 $N_2$도 변하지 않아 거의 평형이 이른 것으로 생각할 수 있다.

비슷하게 보다 일반적으로 $n$개의 동위원소가 계열을 이루어 붕괴를 하여 마지막으로 $n+1$ 번째의 딸원자핵이 되는 상황에서, 다음 조건을 만족한다면 $N_1, ... , N_n$이 모두 평형을 이루어 이들 값들이 거의 변하지 않을 것이다. \[ \boxed{~~ \lambda_1 N_1 = \lambda_2 N_2 = \lambda_3 N_3 = ... = \lambda_{n-1} N_{n-1} = \lambda_n N_n ~~} \]

실제로 $\lambda_1$이 훨씬 작고 나머지들은 상대적으로 큰 값을 갖고 있다면 시간이 흘러서 점차 $N_2, ... , N_n$들이 조금씩 커지면서 위 식이 만족되는 상황이 올 가능성이 생긴다. 그리고 한 번 이 조건에 이르게 되면 각각의 핵의 수가 거의 일정하게 유지되므로 그 상황은 쉽게 흐트러지지 않는다.

앞의 '거듭되는 핵변환'프로그램에서 콤보박스를 통하여 'Radioactive equiv.'를 선택하면 A 부터 계열의 마지막 방사성 동위원소인 I까지의 붕괴상수가 각각 0.00005, 0.1, 0.3, 0.4, 0.05, 0.7, 0.6, 0.9, 0.2의 값을 하고 있는 붕괴계열이 선택된다. 따라서 처음 핵 A는 붕괴확률이 작으며 나머지들은 상대적으로 그 값이 커서 평형에 이를 가능성이 있다. 'run/pause'를 눌러서 시간의 경과에 따른 핵들의 변화를 관찰해 보면 얼마의 시간이 흐른 후 상당히 오랜 시간 동안 거의 방사성 평형이 이루어지고 유지되는 것을 볼 수 있다.

graphic

방사성 평형에 도달_ '거듭되는 핵변환'프로그램에서 'Radioactive equiv.'에 대한 방사성 평형에 거의 이른 상황에서의 각각의 핵의 수를 나타내고 있다. 각각의 핵의 수에 붕괴상수를 곱하면 B ~ I 의 경우 0.495 주변 값을 하고 있는 것을 알 수 있다.

만일에 출발 원자핵이 다른 과정, 예를들어 원자로나 가속기의 인공적인 방법이나 우주공간에서 날아오는 우주선 등에 의해 계속해서 생성되고 있다면 완전한 형태의 평형이 이루어질 수도 있다.

방사성 동위원소를 함유하고 있는 광물질은 지구가 생성되고 오랜 기간이 지나 같은 계열을 이루는 각각의 동위원소들이 평형상태를 유지하는 경우가 많다. 이로부터 붕괴상수가 매우 적어 반감기가 매우 긴 동위원소의 반감기를 측정해 내기도 한다. 예를 들어 우라늄광은 평형상태를 이루고 있는 데 이는 출발 원자핵인 U-238의 붕괴상수가 매우 적기 때문이다. (만일에 U-238의 붕괴상수가 컸다면 생성이 오래된 지금의 지구상에는 거의 남아 있지 않았을 것이다) 우라늄광 속에는 $2.8\times 10^6$개의 U-238 핵에 1개의 비율로 Ra-226이 존재한다. 따라서 $N_U\lambda_U=N_{Ra}\lambda_{Ra}$의 관계나, 혹은 붕괴상수 대신에 반감기로 표시한 이와 대등한 관계 $\frac{N_U}{T_U}=\frac{N_{Ra}}{T_{Ra}}$로부터 U-238의 반감기를 $4.46\times 10^9$년 이라고 알아낼 수 있다. 이 값은 거의 지구의 나이 정도로 길어서 직접 측정하기는 불가능하다. (앞 '4개의 자연 방사성붕괴 계열'의 표에서 우라늄 계열을 선택해 보면 U에서 Ra에 이르는 동안 그 중간에 반감기가 매우 짧은 몇몇 핵들이 있는 것을 알 수 있다. 이들은 붕괴상수가 너무 커서 순간적으로 생겨나서 사라지므로 거의 U에서 Ra가 바로 만들어 지는 것으로 생각할 수 있다. 이 점 때문에 '거듭되는 핵변환' 프로그램에서는 거의 U로부터 마지막 안정된 딸핵 Pb가 바로 만들어지는 것처럼 보인다)

[질문1] '방사선 평형에 도달'의 그림의 상황인 시점에서의 A 핵의 잔존 수는 대략 얼마일까?

_ 방사성 동위원소_ 방사성붕괴_ 붕괴상수_ 방사선_ 반감기_ 딸핵