슈뢰딩거 방정식 |  |
 |
프로그램양자역학의 효과는 초미소 에너지, 초미세 스케일에서 나타나기 때문에 일상생활에서 경험하기 어렵다. 다음 프로그램은 슈뢰딩거 방정식의 지배를 받는 파동함수가 시간 1. 먼저 화면 아래 조절창의 왼편 콤보 박스에서 여러 형태의 퍼텐셜을 설정할 수 있으며 퍼텐셜의 세부적인 값들은 'potential center', 'potential height', 'potential width'의 슬라이드로 조절할 수 있다. 조정내용은 즉시 화면에 반영되어 퍼텐셜의 그림이 맨 위 영역에 나타난다. 2. 초기에 주어지는 파동함수는 다음과 같은 가우스 모양이며 중심은 '
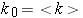 , , 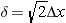 이다. 이다.
3. 시시각각 변하는 파동함수와 운동량공간의 파동함수를 다양한 모양의 그래프로 나타낸다. 위치공간의 파동함수는 위에서 두 번째, 운동량공간의 파동함수는 세 번째에 나타낸다. 이때 복소파동함수를 표현하기 위해 'Abs graph', 'Re and Im graph', 'Probability', 'color image' 등 여러 형태로 볼 수 있도록 하였다. 4. 버튼 "Start/Stop"의 버튼으로 운동을 시작시키거나 중지시킬 수 있다. 5. 양쪽 가장자리는 무한이 높은 퍼텐셜이 있는 것으로 설정하였고, 이에 부딪히면 파동이 반사되어 되돌아 나오게 된다. |
실험방법[1] 자유입자의 운동1. 'Select Thema'에서 'Free Particle'을 선택하여 운동을 시켜보자.
가우스 함수형의 파동함수가 오른쪽으로 진행하면서 점차 파동의 폭이
넓어지는 것을 볼 수 있다. 이는 속박되지 않는 파동묶음의 일반적인 특성이다.
이때 초기 2. ' 3. 'uncertainty 4.
'uncertainty 5. 4에서의 결과 그래프를 분석하여 파동이 퍼지는 정도가 시간에 따라 어떤 특성이 있는지 알아보자.
또한 [2] 터널효과1. 'Select Thema'에서 'Potential Barrier Exp.'을 선택하여 운동을 시켜보자. 입자의 평균운동에너지가 퍼텐셜 장벽보다 작아서 고전입자라면 장벽을 통과하지 못하고 반사되어 튀어 나와야 할 것이다. 2. 3. 퍼텐셜의 폭과 높이를 적절히 조절하여 통과하는 파속의 비율이 이들 값에 어떻게 관련되어 있는지 관찰하자. 이때 입사하는 입자의 비율에 대해 통과하는 입자의 비율은 파동함수의 확률(probability)그래프의 면적을 비교하여 측정할 수 있다. [3] 퍼텐셜 우물1. 'Select Thema'에서 'Potential Well (Free)'를 선택하자. 이 경우는 중심부에 퍼텐셜 우물이 있고, 입자의 평균 에너지는 높게 주어져 있어 우물에 속박되지 않는 자유입자이다. 운동을 시키면 파속이 우물에서 일부 반사되는 것을 확인할 수 있다. 고전입자라면 우물을 그대로 통과해야 할 것이다. 이는 마치 빛이 굴절률이 다른 매질을 통과하면서 일부 반사되는 것과 비슷한 현상이다. 2. 'Select Thema'에서 'Potential Well (Bound)'를 선택하자. 이 경우는 퍼텐셜 우물에 입자가 갇혀있는 상황이다. 운동을 시켜보면 우물의 가장자리에서 일부 바깥으로 침투하는 것을 볼 수 있다. 만일 입자의 평균운동에너지를 적게 주면 가장자리 바깥으로 침투하는 비율이 줄어들 것이다. [4] 퍼텐셜 계단1. 'Select Thema'에서 'Potential Step'을 선택하면 입자의 에너지 보다 두 배 높은 퍼텐셜 계단이 설정된다. 2. 결국에는 파동함수가 거의 전부 되튀어 나오지만 일부 안으로 침투하는 것을 볼 수 있다. 3. 장벽을 높이면 침투하는 깊이가 줄어든다. 이는 마치 바닷물에서 전파가 깊이 침투하지 못하는 것과 비슷한 현상이다. 이때 침투깊이를 표피깊이라 한다. [5] 조화진동자의 운동1. 'Select Thema'에서 'Harmonic Oscillator Exp.'를 선택하면 퍼텐셜이 조화함수의 꼴을 한다. 즉 용수철에 매달린 물체의 운동을 관찰할 수 있다. 2. 고전적인 입자라면 퍼텐셜에너지와 입자의 에너지가 일치하는 지점 사이로 조화운동을 할 것이다. 파동묶음의 운동은 어떤지 관찰하자. 특히 시시각각의 입자의 평균위치를 그래프 화면의 오른쪽 아래의 데이터에서 기록해 보자. 평균위치를 시간의 함수로 그려서 이를 분석해 보자. 3. 2 에서의 결과는 고전적인 입자의 행동과 비교해 보면 거의 일치하는 것을 알 수 있다. 구체적인 비교를 위해서 다음의 단위계에 대한 해석을 참고하라. 4. 조화진동자의 경우 입자의 평균위치, 즉 위치 기대치는 정확하게 단조화운동을 하게 된다. 에른페스트 정리(Ehrenfest theroem)로 잘 알려진 바와 같이 평균위치 <x>와 평균운동량 <p>은 고전 입자의 운동방정식을 만족한다. 즉 이 경우에는 파동묶음이 거의 모양이 흐트러지지 않고 계속 왕복운동 하는 것을 알 수 있는데 속박상황이라도 이러한 일이 다른 퍼텐셜의 경우에는 성립하지 않는다. 이는 화면 왼편의 퍼텐셜 선택창에서 'Linear Potential(V Type)'을 선택해서 같은 측정을 해보면 알 수 있다. [6] 알파입자의 붕괴1. 'Select Thema'에서 'Alpha-decay Exp.'를 선택하면 핵의 구성원으로 들어 있는 알파입자가 핵에 의해 느끼는 퍼텐셜을 설정한다. 알파입자는 핵과의 거리가 가까울 때에는 핵력의 강한 인력이 작용하지만 핵의 범위를 벗어나는 정도에서부터는 양전하 사이의 전기적인 반발력이 먼 거리까지 작용한다. 이 퍼텐셜은 이렇게 핵과 알파입자사이의 퍼텐셜을 단순화시켜 표현한 것이다. 2. 처음에 주어진 조건으로 운동을 시켜보면 오른쪽으로 이동하는 파속의 일부분이 퍼텐셜 장벽을 통과하여 핵 밖으로 빠져나가는 것을 볼 수 있다. 이렇게 알파입자가 핵에서 빠져나오는 현상을 알파붕괴라고 한다. 비록 알파입자가 핵의 인력에 의한 퍼텐셜 장벽을 넘을 수 없는 에너지를 가지고 있더라도 알파붕괴가 일어날 수 있는 것은 양자역학의 중요한 결과이다. 3. '<k>'를 여러 값으로 변화시켜서 알파붕괴가 일어날 확률이 어떻게 달라지는 지를
실험해 보자. 실제의 경우 파동묶음이 한번 장벽에 부딛쳤을 때 그것을 통과할 확률은 매우 낮지만
핵 내부를 계속 왕복하면 그 가능성은 커질 수 있다. 핵에 따라 퍼텐셜의 높이가 다르고, 또한
핵 속에서 알파입자가 놓인 상황이 다르므로 알파붕괴가 일어날 확률은 다르다.
알파붕괴를 하는 대표적인 핵은 [참고] 모의실험의 규모와 실제 물질계의 규모 모의실험에서 사용한 단위계는 길이의 단위 = 10-10m = 0.1 nm 시간의 단위 = 6.59 x 10-16 sec 에너지의 단위 = 1.602 x 10-19 Joule = 1 eV 물론 위와 같은 선택이 절대적인 것이 아니고 다른 선택이 있을 수 있겠다. 그러나 어느 경우든지 우리가 일상생활에서 경험할 수 있는 정도는 아니다. 즉 질량을 크게 Kg 정도로 놓으면 길이가 10-16 nm 정도가 된다든지 아니면 에너지 스케일이 10-30 eV 정도가 되어서 매우 비현실적인 것이 된다. 위에서 잡아준 스케일 정도는 질량이 거의 전자의 4배 정도고 길이가 원자 규모 정도 되는 것이다. 양자효과가 극명하게 나타나는 상황은 그러한 극미세계에서라고 말할 수 있겠다. |
| Copyright ⓒ 1999~ physica.gsnu.ac.kr All rights reserved |  |
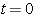 에서
주어졌을 때 시간이 흘러감에 따라 어떤 양상으로 운동해 가는지를 컴퓨터의
수치해석으로 계산하고, 이 결과를 그래프로 표현하게 하였다. 여러가지 다양한 퍼텐셜을
설정할 수 있으며, 또한 몇 가지 주제별 실험을 선택할 수 있다.
에서
주어졌을 때 시간이 흘러감에 따라 어떤 양상으로 운동해 가는지를 컴퓨터의
수치해석으로 계산하고, 이 결과를 그래프로 표현하게 하였다. 여러가지 다양한 퍼텐셜을
설정할 수 있으며, 또한 몇 가지 주제별 실험을 선택할 수 있다.
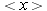 ',
중심 파수는 '
',
중심 파수는 '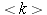 ', 위치의 불확정도는 'uncertainty dx'의 슬라이더로
조절할 수 있다.
', 위치의 불확정도는 'uncertainty dx'의 슬라이더로
조절할 수 있다.
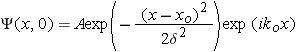
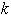 값을 여러가지로 달리하여 파동묶음이 움직이는 속도를 측정하자.
그렇다고 입자가 연기처럼 퍼져 흩어진다는 것은 아니다. 단지 입자를 발견할 확률이
퍼진다는 것이고, 입자를 찾아보면 언제나 한 지점에 있는 것을 확인하게 된다.
값을 여러가지로 달리하여 파동묶음이 움직이는 속도를 측정하자.
그렇다고 입자가 연기처럼 퍼져 흩어진다는 것은 아니다. 단지 입자를 발견할 확률이
퍼진다는 것이고, 입자를 찾아보면 언제나 한 지점에 있는 것을 확인하게 된다.
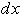 '를 증가시키면 파속의 폭이 넓어지고, 반대로 하면 폭이 좁아진다.
그러나 운동을 시키면 좁은 파속의 경우가 오히려 시간이 흐름에 따라
빨리 흩어지는 특이한 현상을 보인다.
'를 증가시키면 파속의 폭이 넓어지고, 반대로 하면 폭이 좁아진다.
그러나 운동을 시키면 좁은 파속의 경우가 오히려 시간이 흐름에 따라
빨리 흩어지는 특이한 현상을 보인다.
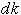 '의 변화를 측정하자. 이때
각각의
'의 변화를 측정하자. 이때
각각의 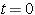 에서의 '
에서의 '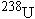 으로 1초에 붕괴가 일어날 확률은
~5 x 10-18정도이다.
으로 1초에 붕괴가 일어날 확률은
~5 x 10-18정도이다.
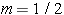 ,
, 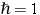 인 것이어서 보통 쓰는
단위계와는 다르지만 길이의 단위, 시간의 단위와 에너지의
단위를 다음과 같이 규정하고 운동하는 입자의 질량을 약 3.48 x 10-30 kg으로
하면 꼭 같은 효과를 거둘 수 있다.
인 것이어서 보통 쓰는
단위계와는 다르지만 길이의 단위, 시간의 단위와 에너지의
단위를 다음과 같이 규정하고 운동하는 입자의 질량을 약 3.48 x 10-30 kg으로
하면 꼭 같은 효과를 거둘 수 있다.