보일-샤를의 법칙 |  |
 |
실험목적많은 입자계가 탄성충돌을 할 때의 부피와 압력 및 온도와의 관계를 측정하여 기체의 보일-샤를의 법칙이 성립하는지를 검증한다. |
이론보일-샤를의 법칙 뉴턴과 비슷한 시기에 살았던 보일(Robert Boyle)은 1662년에
온도가 일정한 조건에서 기체의 부피
한편 이로부터 100년도 더 지난 1800년경에 샤를(J. Charles) 과 게이 뤼삭(Gay-Lussac)은 서로 독립적으로 동일한 압력하의 기체의 부피는 온도에 따라 선형으로 증가하는 것을 발견하였다. 즉 기체는 온도가 1℃ 오를 때 0℃의 부피에 비하여 1/237.15 만큼 부피가 증가하는 것으로 한편으로 온도를 -237.15℃로 내린다면 그 부피가 0이 되는 것을 예측할 수 있었다. 이를 샤를의 법칙이라 하는데 이는 모든 기체의 부피가 0으로 줄어들게 되는 절대적인
온도의 하한이 있다는 것을 말하고 있다. 이 온도의 하한을 새로운 온도 눈금의 기준으로
삼아 0 K 로 삼고 섭씨온도와 같은 간격의 눈금을 매긴 것으로 절대온도를 정하게 되었다.
이 절대온도
이들 관계식은 온도가 극히 낮지 않고 또한 기체의 밀도가 희박한 경우에 잘 성립하는데 언제나 이 법칙을 따르는 가상의 기체를 이상기체라고 한다. 이상기체는 분자의 크기가 거의 0 이어서 용기 속의 공간을 점유하지 않고, 또한 분자끼리의 상호작용이 미치는 거리도 분자들 사이의 평균거리보다 훨씬 적어서 거의 언제나 독립적으로 자유롭게 움직일 수 있는 기체이다. 앞이 두 관계를 하나로 묶어서 쓰면,
이렇게 기체의 압력 따라서 보일-샤를의 법칙은 다음과 같은 이상기체방정식으로 정리할 수 있다.
또한 비례계수
이상기체 법칙은 열역학적인 여러 값들 사이의 관계를 보여주는 하나의 예로서 이것을 보다 일반적으로 상태방정식(equation of state)이라 한다. 즉 열역학적인 변수들은 독립적이지 않고 서로 관련되어 있다는 것을 나타내고 있다. 보일-샤를의 법칙이 나올 당시에는 기체를 구성하는 분자의 존재를 인식하지 못했기 때문에 순전히 경험적인 법칙으로 이해되었지만 이후 기체를 구성하는 분자나 원자의 존재를 알게 되었다. 따라서 이러한 열역학적인 현상들이 분자들의 운동의 결과로 해석할 수 있게 되었다. 아보가드로의 법칙, 즉 온도와 압력이 일정할 때에
같은 부피에 들어있는 분자의 수는 그 종류에 관계없이 일정하다는 법칙을 이용하면
위 이상기체 법칙은 보편적인 것으로 이해할 수 있다.
분자 1 mol 에 들어있는 분자의 수인
아보가드로 수
여기서 19세기 후반에 들어 열적인 현상을 분자 운동의 결과로 명확하게 인식하게 되고,
따라서 많은 수의 입자들의 미시적인 행동을 다루는 통계역학의
성립에 결정적인 역할을 하게 된 오스트리아의 물리학자
볼츠만(Ludwig Boltzmann)의
업적으로
|
| Copyright ⓒ 1999~ physica.gsnu.ac.kr All rights reserved |  |
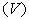 가 압력
가 압력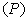 에 반비례한다는
것을 발견하였다. 즉 기체의 부피와 압력의 곱한 값은 동일한
기체에 대해서 다음과 같이 상수값을 갖게 되고 이 관계를 보일의 법칙이라 한다.
에 반비례한다는
것을 발견하였다. 즉 기체의 부피와 압력의 곱한 값은 동일한
기체에 대해서 다음과 같이 상수값을 갖게 되고 이 관계를 보일의 법칙이라 한다.
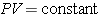
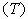 와 부피
와 부피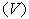 사이의 관계는 다음과 같이 표현된다.
사이의 관계는 다음과 같이 표현된다.
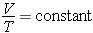
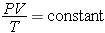
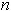 에 비례한다는 것을 알 수 있다.
에 비례한다는 것을 알 수 있다.
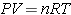
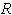 을 보편기체상수(universal gas constant)라 하며,
이는 실험으로 정해지는 양으로 다음과 같다.
을 보편기체상수(universal gas constant)라 하며,
이는 실험으로 정해지는 양으로 다음과 같다.
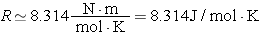
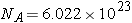 를 이용하면,
이상기체 법칙은 다음과 같이 표현할 수 있게 된다.
를 이용하면,
이상기체 법칙은 다음과 같이 표현할 수 있게 된다.
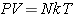
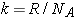 이다.
이다.
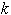 는 새롭고 중요한 의미를 부여받게 되었다.
이를 볼츠만 상수라 하는데
빛의 속도, 플랑크 상수, 만유인력 상수와 더불어
우주를 구성하는 보편적인 상수로 취급된다.
현재까지 알려진 이 값을 자세히 표현하면 다음과 같다.
는 새롭고 중요한 의미를 부여받게 되었다.
이를 볼츠만 상수라 하는데
빛의 속도, 플랑크 상수, 만유인력 상수와 더불어
우주를 구성하는 보편적인 상수로 취급된다.
현재까지 알려진 이 값을 자세히 표현하면 다음과 같다.