|
1. 먼저 콤보 박스에서 테마를 선택한다. 여러 가지의 퍼텐셜을 도입할 수 있게 하며 세부적인 값들은 바로 믿의 스핀컨트롤에 의해 조정된다. 조정내용은 즉시 화면에 반영되어 퍼텐셜의 그림이 오른편 위 영역에 나타난다. 2. "Initial Wave" 패널의 값을 조정하여 초기 파동함수의 값들을 변경할 수 있다. 여기서의 파동속은 다음과 같은 형태의 가우스함수이고, 값을 조정함으로서 가우스 함수의 폭, 중심운동에너지 등을 조정할 수 있고 역시 그 결과는 오른편 그림 패널의 하단부에 그림으로 나타난다.
3. 그림에서의 파동함수는 복소수 값으로 이의 절대치 제곱인 확률밀도를 그래프로, 복소수값의 위상의 부호를 아래 좁은 띄 부분에 적색과 청색으로 나타 내었다. 4. 오른편 아래에 있는 버튼 "Run"을 누르면 파동함수의 운동모습이 계산되어 나타난다. 5. 양쪽 가장자리는 무한이 높은 퍼텐셜이 있는 것으로 거기 부딪히면 반사되어 되돌아 나오게 된다. |
|
|
|
앞의 1차원에서의 슈뢰딩거 방정식에서 h = 1, m = 1/2 의 단위계를 택하고 공간 x를 e, 시간 t를 d의 간격을 갖는 격자로 나누어 x = ej, t = dn으로 한다. 그러면 공간과 시간의 함수는 정수값 j, n에 의존하는 형태가 된다. 공간격자점 j는 아랫첨자로, 또한 시간격자점 n은 윗첨자로 나타내어 파동함수의 경우 ynj처럼 표기하기로 하자. 그러면 앞의 슈뢰딩거 방정식은 다음과 같이 근사형태로 나타낼 수 있다.
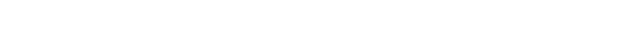
여기서 l = d/e2이다. 실제 연속함수를 미분하는 경우 이를 유한한 간격을 갖는 격자점에서의 함수값으로 오차 없이 계산하기란 불가능하다. 근사적으로 미분을 계산하는데는 여러가지 방법이 있겠고 나름대로 장단점을 가지고 있다. 또한 근사차수를 높이면 오차는 줄어들겠으나 계산이 거의 불가능할 정도로 복잡해진다. 또한 (1)식을 초기시간에서의 (x,t0)로부터 임의의 시간이 지난 후의 (x,t)를 구하는 것으로 이해할 때 그 시간차에 해당하는 시간격자마다 순차적으로 (x,t')를 계산하여야 하므로 오차가 누적될 수 있다. 위 (2)식으로 표현한 근사는 비교적 수렴 및 안정성이 만족스러웠다. 거기따른 이론적인 부분은 수치해석책들에 잘 나와 있고 또한 본 논문으로 다루기에는 너무나 번거롭기 때문에 생략하도록 한다. 한편 공간격자간격 e = 0.005로 하고 시간격자간격 d = 0.0025로 하였고 초기 파동속은 가우스 모양으로 적당한 속도로 움직이는 것을 택하였다. 그러나 위의 조건들은 간단하게 변화시킬 수 있게 하여 여러가지 경우에 대하여 바로 그림으로 그 결과를 볼 수 있도록 하였다. 그리고 x 값의 범위도 0 ~ 2 정도로 잡을 수 있도록 공간격자수는 400정도로 프로그램 하였다. 위 식은 퍼텐셜 Vj가 주어져 있고 또한 시간격자점 n에서의 파동함수 yjn 들이 각각의 j에 대하여 주어져 있을때에는 바로 뒤 시간격자점 n+1 에서의 파동함수 yjn+1를 구할수 있게 한다. 단 이때에 가장자리에서의 파동함수가 0이 되어야 한다는 조건이 있어야 하는데 이 제한이 결국은 계가 전체적으로 무한히 높은 퍼텐셜 장벽에 같혀 있는 상황을 만들게 한다. (대신에 주기적인 경계조건을 인위적으로 줄 수 도 있을 것이나 실제로 파동함수가 가장자리까지 도달하지 않는 범위내에서 계산을 할 것이기 때문에 큰 관계는 없다.) 각각의 공간격자점 j에 대한 y는 1차 연립 방정식 형태가 되어 행렬식으로 풀이 할 수 있다. 한편 초기에 주어지는 파동함수는 가우스함수 형태로서 다음과 같이 표현된다.
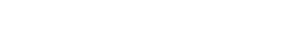
여기서 x0는 파동속의 중심위치이고 는 퍼짐의 정도를 나타낸다. 또한 k0 은 파수로서 양으로 놓으면 파가 왼편에서 오른편으로 이동하는 것을 나타내고 또한 값이 크면 빨리 이동하게 된다. 여기서 플랑크 상수 를 1로 놓았기 때문에 k값 자체가 바로 입자의 운동량이 된다. 그러나 이 식을 운동량 공간으로 푸리에 변환을 하더라도 역시 가우스 형태가 되는데 그 중심 위치가 k0이라는 정도일 뿐 역시 k 값 자체도 1/s 정도의 폭을 가지고 있다. 보통 양자역학에서 퍼텐셜 계단등을 다루는 경우 입사하는 입자의 에너지는 단일한 값으로 주어지게 되어 운동량이 특정한 값이 되고 또한 공간적으로는 무한히 펼쳐진 모양이 되어 실제 상황과 동 떨어진 것이 된다. 여기서는 k 값이 확정적으로 주어지지 못하므로 에너지도 역시 단일한 값으로 주어지지 않는다. 일반 양자역학 교재에 1차원의 갇혀있는 계로 고유상태를 계산할 수 있는 대표적인 것으로서 조화진동자가 빠짐없이 소개되어 있다. 그 경우 파동함수는 파동의 정상파 경우와 같이 일정한 에너지, 즉 고유에너지를 띄엄띄엄한 값으로 갖고 있다. 대부분의 양자역학 교재가 설명하는 바는 어떤상태에 있는 입자는 그 고유상태중의 한 단일상태인 것으로, 이것이 고전적인 조화진동자의 서술과 크게 차이나는 점으로 지적한다. 그러나 그러한 설명은 여러가지 착각을 불러일으키게 하여 양자계를 마치 입자의 움직임이 없는 정체된 것으로 잘못 이해하게 하기도 한다. 그 설명이 완전히 틀렸다고는 말 할 수는 없지만 이는 극히 제한된 조건, 즉 유일한 값의 에너지를 갖는 경우에 맞는 이야기일 뿐이다. 임의의 상태의 양자계는 그러한 공명상태의 에너지값을 갖는 여러 고유상태의 중첩된 상태이기 때문에 실제로 어떤 시간에서 파동함수의 모양은 아무렇게나 되어 있어도 관계없다. 단 어떤 이상적인 실험장치로서 에너지 값을 측정했을때는 고유에너지들의 평균치가 측정되는 것이 아니고 그중 어떤 한 고유에너지값만이 측정된다. 이 모의실험에서의 스케일과 실제 물질계의 스케일실제 본 모의실험에서 사용한 단위계는 m=1/2, h=1인 것이어서 보통 쓰는 단위계와는 실제의 스케일과 다르지만 길이의 단위, 시간의 단위와 에너지의 단위를 다음과 같이 규정하고 운동하는 입자의 질량을 약 3.48 x 10-30 Kg으로 하면 꼭 같은 효과를 거둘 수 있다. 길이의 단위 = 10-10m = 1 A 시간의 단위 = 6.59 x 10-16 sec (4) 에너지의 단위 = 1.602 x 10-19 Joule = 1 eV 물론 위와 같은 선택이 절대적인 것이 아니고 다른 선택이 있을 수 있겠다. 그러나 어느 경우든지 우리가 일상생활에서 경험할 수 있는 정도는 아니다. 즉 질량을 크게 Kg 정도로 놓으면 길이가 10-15 A 정도가 된다든지 아니면 에너지 스케일이 10-30 eV 정도가 되어서 매우 비 현실적인 것이 된다. 위에서 잡아준 스케일 정도는 질량이 거의 전자의 4배정도고 길이가 원자 규모정도 되는 것이다. 양자효과가 극명하게 나타나는 상황은 그러한 극미세계에서라고 말할 수 있겠다. 조화진동자의 운동조화진동자의 경우 입자의 평균위치, 즉 위치 기대치는 정확하게 단조화 운동을 하게된다. 에른페스트 정리로 잘 알려진 바와 같이 평균위치 <x>와 평균운동량 <p>은 고전 입자의 운동방정식을 만족한다. 이를 위 프로그램을 운용해 봄으로서 확인할 수 있을 것이다. 즉 이 경우에는 파동속이 거의 모양이 흐트러지지 않고 계속 왕복운동 하는 것을 알 수 있는데 속박상황이라도 이러한 일이 다른 퍼텐셜의 경우에는 성립하지 않음을 1차나 3차 퍼텐셜로 부너 확인 할 수 있을 것이다. 참고자료1) 정기수, 최홍수, 1990, "갇혀있는 파동속의 운동에 대한
양자역학적 모의 실험", 경상대학교 과학교육연구소보, 10, 11-18.
|
|
|
